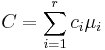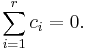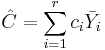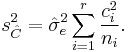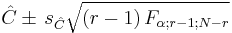Scheffé's method

In statistics, Scheffé's method, named after Henry Scheffé, is a method for adjusting significance levels in a linear regression analysis to account for multiple comparisons. It is particularly useful in analysis of variance, and in constructing simultaneous confidence bands for regressions involving basis functions.

Scheffé's method is a single-step multiple comparison procedure which applies to the set of estimates of all possible contrasts among the factor level means, not just the pairwise differences considered by the Tukey–Kramer method.

Let μ1, ..., μr be the means of some variable in r disjoint populations.

An arbitrary contrast is defined by

C = \sum_{i=1}^r c_i\mu_i

where

\sum_{i=1}^r c_i = 0.

If μ1, ..., μr are all equal to each other, then all contrasts among them are 0. Otherwise, some contrasts differ from 0.

Technically there are infinitely many contrasts. The simultaneous confidence coefficient is exactly 1 − α, whether the factor level sample sizes are equal or unequal. (Usually only a finite number of comparisons are of interest. In this case, Scheffé's method is typically quite conservative, and the experimental error rate will generally be much smaller than α.)[1][2]

We estimate C by

\hat{C} = \sum_{i=1}^r c_i\bar{Y}_i

for which the estimated variance is

s_{\hat{C}}^2 = \hat{\sigma}_e^2\sum_{i=1}^r \frac{c_i^2}{n_i}.

It can be shown that the probability is 1 − α that all confidence limits of the type

\hat{C}\pm\,s_\hat{C}\sqrt{\left(r-1\right)F_{\alpha;r-1;N-r}}

are correct simultaneously.

Comparison with the Tukey–Kramer method

If only pairwise comparisons are to be made, the Tukey–Kramer method will result in a narrower confidence limit, which is preferable. In the general case when many or all contrasts might be of interest, the Scheffé method tends to give narrower confidence limits and is therefore the preferred method.

References

  1. ^ Scott E. Maxwell and Harold D. Delaney. Designing Experiments and Analyzing Data: A Model Comparison. Lawrence Erlbaum Associates, 2004, ISBN 0805837183, pp. 217–218.
  2. ^ George A. Milliken and Dallas E. Johnson. Analysis of Messy Data. CRC Press, 1993, ISBN 0412990814, pp. 35–36.

External links

 This article incorporates public domain material from websites or documents of the National Institute of Standards and Technology.